15. Dynamic Flux Balance Analysis (dFBA) in COBRApy¶
The following notebook shows a simple, but slow example of implementing dFBA using COBRApy and scipy.integrate.solve_ivp. This notebook shows a static optimization approach (SOA) implementation and should not be considered production ready.
The model considers only basic Michaelis-Menten limited growth on glucose.
[1]:
import numpy as np
from tqdm import tqdm
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
%matplotlib inline
Create or load a cobrapy model. Here, we use the ‘textbook’ e-coli core model.
[2]:
import cobra
from cobra.io import load_model
model = load_model('textbook')
Scaling...
A: min|aij| = 1.000e+00 max|aij| = 1.000e+00 ratio = 1.000e+00
Problem data seem to be well scaled
15.1. Set up the dynamic system¶
Dynamic flux balance analysis couples a dynamic system in external cellular concentrations to a pseudo-steady state metabolic model.
In this notebook, we define the function add_dynamic_bounds(model, y) to convert the external metabolite concentrations into bounds on the boundary fluxes in the metabolic model.
[3]:
def add_dynamic_bounds(model, y):
"""Use external concentrations to bound the uptake flux of glucose."""
biomass, glucose = y # expand the boundary species
glucose_max_import = -10 * glucose / (5 + glucose)
model.reactions.EX_glc__D_e.lower_bound = glucose_max_import
def dynamic_system(t, y):
"""Calculate the time derivative of external species."""
biomass, glucose = y # expand the boundary species
# Calculate the specific exchanges fluxes at the given external concentrations.
with model:
add_dynamic_bounds(model, y)
cobra.util.add_lp_feasibility(model)
feasibility = cobra.util.fix_objective_as_constraint(model)
lex_constraints = cobra.util.add_lexicographic_constraints(
model, ['Biomass_Ecoli_core', 'EX_glc__D_e'], ['max', 'max'])
# Since the calculated fluxes are specific rates, we multiply them by the
# biomass concentration to get the bulk exchange rates.
fluxes = lex_constraints.values
fluxes *= biomass
# This implementation is **not** efficient, so I display the current
# simulation time using a progress bar.
if dynamic_system.pbar is not None:
dynamic_system.pbar.update(1)
dynamic_system.pbar.set_description('t = {:.3f}'.format(t))
return fluxes
dynamic_system.pbar = None
def infeasible_event(t, y):
"""
Determine solution feasibility.
Avoiding infeasible solutions is handled by solve_ivp's built-in event detection.
This function re-solves the LP to determine whether or not the solution is feasible
(and if not, how far it is from feasibility). When the sign of this function changes
from -epsilon to positive, we know the solution is no longer feasible.
"""
with model:
add_dynamic_bounds(model, y)
cobra.util.add_lp_feasibility(model)
feasibility = cobra.util.fix_objective_as_constraint(model)
return feasibility - infeasible_event.epsilon
infeasible_event.epsilon = 1E-6
infeasible_event.direction = 1
infeasible_event.terminal = True
15.2. Run the dynamic FBA simulation¶
[4]:
ts = np.linspace(0, 15, 100) # Desired integration resolution and interval
y0 = [0.1, 10]
with tqdm() as pbar:
dynamic_system.pbar = pbar
sol = solve_ivp(
fun=dynamic_system,
events=[infeasible_event],
t_span=(ts.min(), ts.max()),
y0=y0,
t_eval=ts,
rtol=1e-6,
atol=1e-8,
method='BDF'
)
t = 5.804: : 185it [00:05, 34.89it/s]
Because the culture runs out of glucose, the simulation terminates early. The exact time of this ‘cell death’ is recorded in sol.t_events.
[5]:
sol
[5]:
message: 'A termination event occurred.'
nfev: 179
njev: 2
nlu: 14
sol: None
status: 1
success: True
t: array([0. , 0.15151515, 0.3030303 , 0.45454545, 0.60606061,
0.75757576, 0.90909091, 1.06060606, 1.21212121, 1.36363636,
1.51515152, 1.66666667, 1.81818182, 1.96969697, 2.12121212,
2.27272727, 2.42424242, 2.57575758, 2.72727273, 2.87878788,
3.03030303, 3.18181818, 3.33333333, 3.48484848, 3.63636364,
3.78787879, 3.93939394, 4.09090909, 4.24242424, 4.39393939,
4.54545455, 4.6969697 , 4.84848485, 5. , 5.15151515,
5.3030303 , 5.45454545, 5.60606061, 5.75757576])
t_events: [array([5.80191035])]
y: array([[ 0.1 , 0.10897602, 0.11871674, 0.12927916, 0.14072254,
0.15310825, 0.16649936, 0.18095988, 0.19655403, 0.21334507,
0.23139394, 0.25075753, 0.27148649, 0.29362257, 0.31719545,
0.34221886, 0.36868605, 0.3965646 , 0.42579062, 0.4562623 ,
0.48783322, 0.52030582, 0.55342574, 0.58687742, 0.62028461,
0.65321433, 0.685188 , 0.71570065, 0.74425054, 0.77037369,
0.79368263, 0.81390289, 0.83089676, 0.84467165, 0.85535715,
0.8631722 , 0.86843813, 0.8715096 , 0.8727423 ],
[10. , 9.8947027 , 9.78040248, 9.65642157, 9.52205334,
9.37656372, 9.21919615, 9.04917892, 8.86573366, 8.6680879 ,
8.45549026, 8.22722915, 7.98265735, 7.72122137, 7.442497 ,
7.14623236, 6.83239879, 6.50124888, 6.15338213, 5.78981735,
5.41206877, 5.02222068, 4.62299297, 4.21779303, 3.81071525,
3.40650104, 3.01042208, 2.6280723 , 2.26504645, 1.92656158,
1.61703023, 1.33965598, 1.09616507, 0.88670502, 0.70995892,
0.56344028, 0.44387781, 0.34762375, 0.27100065]])
y_events: [array([[0.87280538, 0.25178492]])]
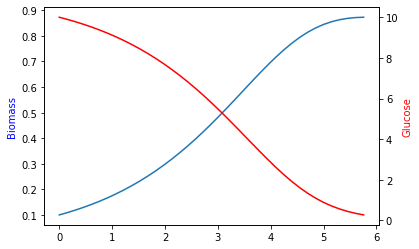
15.2.1. Plot timelines of biomass and glucose¶
[6]:
ax = plt.subplot(111)
ax.plot(sol.t, sol.y.T[:, 0])
ax2 = plt.twinx(ax)
ax2.plot(sol.t, sol.y.T[:, 1], color='r')
ax.set_ylabel('Biomass', color='b')
ax2.set_ylabel('Glucose', color='r')
[6]:
Text(0, 0.5, 'Glucose')
[ ]: